Câu hỏi cát tuyến là gì chính là thắc mắc của nhiều bạn khi đang học toán hình. Trong bài viết này Thợ sửa xe sẽ giải đáp các thắc mắc liên quan đến vấn đề này để bạn có thể giải quyết các bài tập liên quan một cách dễ dàng nhất nhé!
Định nghĩa đường cát tuyến là gì?
Như chúng ta đã biết thì môn toán, đặc biệt là toán hình là môn học vô cùng quan trọng bởi nó có tính ứng dụng rất cao trong cuộc sống. Nó được xem là môn học bắt buộc và xuất hiện rất nhiều trong các bài học và bài thi của học sinh. Trong đó, kiến thức liên quan đến cát tuyến là gì chính là câu hỏi được quan tâm tìm kiếm rất nhiều trong thời gian qua. Cụm từ cát tuyến được sử dụng nhiều trong bài tập, bài thi nên việc tìm hiểu để biết rõ là rất cần thiết.
Cát tuyến là một từ mượn Hán Việt. Cụ thể trong đó từ “cát” có nghĩa là cắt, giao còn “tuyến” là từ để chỉ đường thẳng. Bởi vậy, cát tuyến chính là thuật ngữ để chỉ một đường thẳng cắt hoặc giao với các đường khá, cụ thể là: Đường thẳng, đường cong, đường tròn,…

Vậy cát tuyến đường tròn là gì? Theo khái niệm đã được nêu trong sách giáo khoa lớp 9 bộ môn toán thì cát tuyến chính là một đường thẳng và đường thẳng này sẽ cắt với một đường thẳng khác. Cát tuyến đường tròn chính là 1 đường thẳng và nó sẽ cắt đường tròn đó tại hai điểm phân biệt. Còn cát tuyến của 2 đường thẳng sẽ là 1 đường thẳng cắt với 2 đường thẳng trên. Bên cạnh đó cũng có 1 vài trường hợp đặc biệt như cát tuyến đi qua tâm của đường tròn.
Bài tập liên quan đến cát tuyến của đường tròn
Nhờ những giải thích chi tiết ở trên thì hẳn là bạn đã hiểu rõ hơn về ý nghĩa của đường cát tuyến đang được sử dụng rất nhiều trong các bài tập toán hình hiện nay rồi phải không nào? Vậy để hiểu rõ hơn nữa về nghĩa của nó thì chúng ta cũng cần phải tìm hiểu rõ về các ví dụ cụ thể của đường cát tuyến.
Ví dụ đối với cát tuyến của 1 đường tròn ta có bài tập tiêu biểu như sau: Từ 1 điểm M nằm bên ngoài đường tròn (O) hãy vẽ 1 đường cát tuyến MCD không đi qua tâm O và có hai tiếp tuyến lần lượt là MA và MB đến đường tròn (O). Ở đây A, B chính là các tiếp điểm và C sẽ nằm giữa M, D.
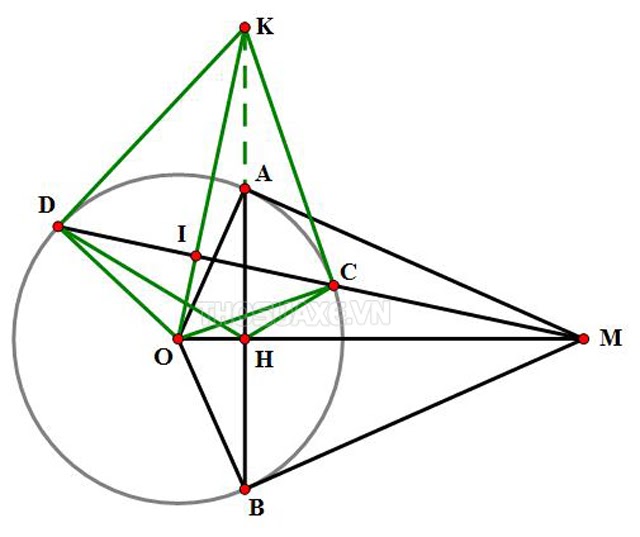
1) Chứng minh rằng: MA.MA = MC.MD.
2) Gọi I chính là trung điểm của đoạn CD. Chứng minh rằng 4 điểm M, A, O, I, B cùng nằm bên trên 1 đường tròn.
3) Gọi H là giao điểm của 2 đường thẳng HB và MO. Chứng minh rằng tứ giác CHOD nội tiếp với (O) và HB chính là đường phân giác của góc CHD.
4) Gọi K là giao điểm của các tiếp tuyến lần lượt tại C và D của đường tròn (O). Chứng minh rằng 3 điểm A, B, K cùng nằm trên 1 đường thẳng.
Giải bài tập liên quan đến cát tuyến của đường tròn
Với bài tập bên trên, mời các bạn tham khảo cách giải dưới đây để có thể hiểu hơn về đường cát tuyến nhé!
- Vì MA chính là tiếp tuyến của (O) nên chúng ta có:
-> Góc MAC = Góc MDA -> ΔMAC ~ ΔMDA (g.g)
-> MA/MD = MC/MA -> MA.MA = MC.MD
- Vì I là trung điểm của CD
Suy ra góc MIO = 90 độ = góc MAO = góc MBO. Từ đây ta có thể kết luận được M, A, O, I, B sẽ cùng nằm trên 1 đường tròn.
- Vì ta có: MA vuông góc với OA, OM vuông góc với OB tại điểm H. Suy ra MH.MO = MA.MA = MC.MD
-> MA/MD = MC/MA -> ΔMHC ~ ΔMDC -> Góc MHC = góc MDO
Suy ra tứ giác HDCO là tứ giác nội tiếp
-> Góc OHD = góc OCD = góc ODC = góc MHC
-> 90 độ – góc MHC = 90 độ – góc OHD -> góc CHB = góc BHD
Kết luận: HB chính là phân giác của góc CHD.
HB là phân giác của góc CHD
- Vì KC, KD lần lượt là tiếp tuyến của (O)
-> KCOD là tứ giác nội tiếp (O) mà HOCD cũng là tứ giác nội tiếp (chứng minh trên). Như vậy 4 điểm K, C, H, O, D cùng thuộc 1 đường tròn.
Mà HK là phân giác của góc CHD do KC = KD
Suy ra, 3 điểm A, B, K thẳng hàng.
Trên đây Thợ sửa xe đã chia sẻ tới các bạn đọc bài cát tuyến là gì cũng như tìm hiểu thêm về bài tập có liên quan đến cát tuyến của đường tròn. Hy vọng với những kiến thức bổ ích này sẽ giúp các bạn hiểu được các định nghĩa của bài tập và từ đó vận dụng nhuần nhuyễn để giải bài tập toán có liên quan đến cát tuyến một cách hiệu quả và nhanh chóng nhất. Chúc các bạn học tập thật tốt và nhớ thường xuyên tương tác với chúng tôi để có thể đọc được nhiều thông tin hay và bổ ích nhé.
